1.
3 points questions
How much is 12 + 23 + 34 + 45 + 56 + 67 + 78 + 89?
2.
How many axes of symmetry does the figure have?

3.
oy kangaroos are packed for shipment. Each of them is packed in a box,which is a cube. Exactly eight boxes are packed tightly in a bigger cubic cardboard box. How many kangaroo boxes are on the bottom floor of this big cube?
4.
The perimeter of the figure is equal to...

5.
Eleanor draws the six vertices of a regular hexagon and then connects some of the 6 points with lines to obtain a geometric figure. Then this figure is surely not a...

6.
If we type seven consecutive integer numbers and the sum of the smallest three numbers is 33, what is the sum of the largest three numbers?
7.
After stocking up firewood, the worker summed up that from acertain number of logs he made 72 logs with 53 cuts. He saws only one log at a time. How many logs were there at the beginning?
8.
There are seven bars in the box. They are 3 cm × 1 cm in size. The box is of size 5 cm × 5 cm. Is it possible to slide the bars in the box so that there will be room for one more bar? At least how many bars must be moved to accomplish this?

9.
A square is divided into 4 smaller equal-sized squares. All the smaller squares are coloured in dark and light grey. How many different ways are there to colourthe given square? (Two colourings are considered the same if one can be rotated to give the other, as shown)

10.
The sum of the first hundred positive odd integers subtracted from the sum of the first hundred positive even integers is
11.
4 points questions
Grandma baked a cake for her grandchildren who will visitherin the afternoon. Unfortunately she forgot whether only 3, 5 or all 6 of her grandchildren will come over. She wants to ensure that every child gets the same amount of cake. Then, to be prepared for all three possibilities she better cut the cake into
12.
Which of the following is the smallest two-digit number that is not the sum of three different one-digit numbers?
13.
Cathy needs 18 min to make a long chain by connecting three short chains with extra chain links. How long does it take her to make a really long chain by connecting six short chains in the same way?
14.
In quadrilateral ABCD we have AD= BC, DAC= 50º, DCA= 65º, ACB= 70º (see the fig.). Find the value of angle ABC

15.
Andrea has wound some rope around a piece of wood. She rotates the wood as shown with the arrow.
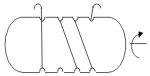
Front side
What is the correct back side of the piece of wood?
Back side:
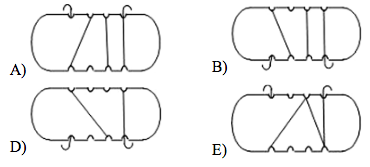

16.
There are 50 bricks of white, blue and red colour inabox. The number of white bricks is eleven times the number of blue ones. There are fewer red ones than white ones, but more red ones than blue ones.How many fewer red bricks are there than white ones?
17.
On the picture ABCDis a rectangle, PQRSis a square. The shaded area is half of the area of rectangle ABCD. What is the length of the PX?

18.
What is the smallest number of straight lines needed to divide the plane into exactly 5 regions?
19.
If a–1 = b+ 2 = c–3 = d+ 4 = e–5, then which of the numbers a, b, c, d, e is the largest?
20.
The logo shown is made entirely from semicircular arcs of radius 2 cm, 4 cm or 8 cm. What fraction of the logo is shaded?

21.
5 points questions
In the figure there are nine regions inside the circles. Put all the numbers from 1 to 9 exactly one in each region so that the sum of the numbers inside each circle is 11.
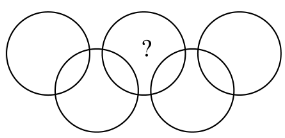
Which number must be written in the region with the question mark?
22.
At a barter market, the goods have to be exchanged according to the price list stated in the chart. At least how many hens doesMr. Blackhave to bring to the market, to be able to take away one goose, one turkey and one cock?

23.
A paper strip was folded three times in half and then completely unfolded so that you can still see the 7 folds going up or down. Which of the following views from the side cannot be obtained in this way?

24.
On each of 18 cards exactly one number is written, either 4 or 5. The sum of all numbers on the cards is divisible by 17. On how many cards is the number 4 written?
25.
The natural numbers from 1 to 10 are written on the blackboard. The students in the class play the following game: a student deletes 2 of the numbers and instead of them writes on the blackboard their sum decreased by 1; after that another student deletes 2 of the numbers and instead of them writes on the blackboard their sum decreased by 1; and so on. The game continues until only one number remains on the blackboard. The last number is:
26.
In a town there are only knights and liars. Every sentence spoken by a knight is true, every sentence spoken by a liar is false. One day some citizens were in a room and three of them spoke as follows:1) The first one said: «There are no more than three of us in the room. All of us are liars». 2) The second said: «There are no more than four of us in the room. Not all of us are liars». 3) The third said: «There are five of us in the room. Three of us are liars. How many people are in the room and how many liars are among them?
27.
A Kangaroo has a large collection of small cubes 1 × 1 × 1. Each cube is a single colour. Kangaroo wants to use 27 small cubes to make a 3 × 3 × 3 cube so that any two cubes with at least one common vertex are of different colours. At least how many colours have to be used?
28.
The biggest equilateral triangle consists of 36 smaller equilateral triangles with area 1 cm
2 each. Find the area of ∆ABC

29.
Five friends have each21, 32, 17, 11 and16 candies. They want to give some candies to another friend. What is the minimum number of candies that they can give so that the initial group of five friends could share equally the candies between them?
30.
In the figure, α= 7° and the segments OA
1,A
1A
2, A
2A
3, ... are all equal. The lengths OA form a numerically increasing sequence. What is the greatest number of segments that can be drawn in this way?
