1.
3 POINTS FOR EACH PROBLEM
Contest Math Kangaroo takes place in Europe every year since1991. In year 2006 it will be the. . . contest.
2.
20×(0 + 6)−(20×0) + 6 =
3.
Point O is the center of the regular pentagon. What part of the whole pentagon is the shaded region?

4.
Two sides of a triangle are 120 and 130 inches long. Which of the following numbers below could not be the length of the third side of the triangle?
5.
2006 students participated in a survey. The survey stated that 1500 of them participated in the Math Kangaroo Contest, and 1200 of them participated in an English Language Contest. Out of the students who participated in the survey, how many participated in both contests if it’s known that 6 people did not take part in any of the competitions?
6.
A solid is made out of two cubes with edges 1 inch and 3 inches. What is the surface area of the solid in square inches?

7.
A bottle of a volume of 1/3 liter is 3/4 filled with juice. How much juice will be left in the bottle after pouring out 1/5 of a liter?
8.
Out of isosceles triangles with sides of 7, and a base with the length expressed by whole number,the triangle with the greatest perimeter was selected. This perimeter is equal to:
9.
Granny baked dumplings for her grandchildren. If she gave each one of them 2 dumplings, she would still have 3 more left, but if she gave each one of them 3 dumplings, she would be short by two. How many grandchildren does she have?
11.
4 POINTS FOR EACH PROBLEM
How many non-negative whole numbers smaller than 100 can youget as a sum of nine consec-utive whole numbers?
12.
In some month three Tuesdays came out to be on even days of the month. Which day of the week will be the 21st day of that month?
13.
Mark, Matthew, and Peter were saving money to buy a tent. Markhad 60% of the needed sum, and Matthew gave 40% of the remaining amount. Peter gave30 dollars to complete the sum.How much was the tent?
14.
A group of aliens was traveling in a spaceship. Each one of them was dressed in a jumpsuit that was of one of the following colors: green, orange, or blue. Each alien dressed in a green jump suit had two tentacles, each alien dressed in an orange suit had three tentacles, and each alien dressed in a blue jumpsuit had five tentacles. There were as many aliens dressed in green suits as those dressed in orange, and there were 10 more aliens dressed in blue than those dressed in green. Allaliens together had 250 tentacles. How many aliens were dressed in blue?
15.
When Jumpy, the Kangaroo, jumps on his left foot his jump is 2 feet long and when he jumpson his right foot then his jump is 4 feet long. If Jumpy jumps using his both feet, then his jumpsare 7 feet long. What is the smallest number of jumps that Jumpy must make to travel exactly1000 feet?
16.
A rectangle is divided into 7 squares. The sides of the grey squares on the right are all 8 unites long. What is the side of the big white square?

17.
A square of a positive number is 500% greater than that number. What number is it?
18.
In isosceles triangle ABC, with side|AC|=|BC|, angle BAC has been bisected by|AD|(look at the figure), and,|AD|=|AB|. What is the measure of angle ∠ACB

19.
Barbara is creating different squares with sticks of equal length. She numbers them with numbers 1, 2, 3 etc. How many more sticks will she use to create 31
st square than the 30
th square?

20.
The digit of ones of a certain three-digit number is 2. If we move this digit to the beginningof that number, as a result we will get a three digit number that is smaller than the original one by36. What is the sum of the digits of that number?
21.
5 POINTS FOR EACH PROBLEM
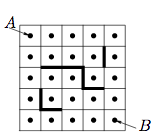
Helen drew a 5×5-square and marked centers of each small square.Afterwards, she drew obstacles and then she tested in how many ways itwas possible to move from A to B in the shortest possible way avoidingthe obstacles, and moving vertically or horizontally from center to center of each small square. How many possible paths of the shortest length are there?
22.
A train consists of a locomotive and five cars marked I, II, III, IV and V. In how many wayscan you rearrange the cars, in such way that car I is always closer to the locomotive than car II?
23.
What is the first digit of the smallest natural number that sum of its digits equals 2006?
24.
How many isosceles triangles with area of 1 have a side with it’s length equal to 2?
25.
Peter rides a bicycle from town P to town Q with a constant speed. If he increases his speed by 3 m/s, he will arrive to town Q 3 times faster. How many times faster will Peter arrive to town Q, if he increases his speed by 6 m/s?
26.
If the product of two integers equals 25 x 3 x 52 x 73, then their sum can be:
27.
Let ABCD be a square with the length of side equal to 12 inches. Points P, Q, Rare respectively the midpoints of sides BC,CD, and DA, respectively(see figure).
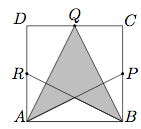
The area of the shaded region in square inches is equal to
28.
The first row shows 11 cards, each with 2 letters. The second row shows rearrangement of the cards from the first row. Which of the following could appear on the bottom line of the second row?

29.
What is the value of this expression:(12+ 22+ 32+. . .+ 20052)−(1×3 + 2×4 + 3×5 +. . .+ 2004×2006)?
30.
Let x,y, and z be positive real numbers and let x≥ y≥ z so that x+y+z= 20.1. Which of the following statements is true?