1.
Part A: Each correct answer is worth 3 points
When the letters of the word MAMA are written vertically above one another, the word has a verticalline of symmetry. Which of these words also has a vertical line of symmetry when written in the same way?
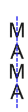
2.
A triangle has sides of length 6, 10 and 11. An equilateral triangle has the same perimeter. What is the length of each side of the equilateral triangle?
3.
Which number should replace ∗ in the equation 2 ∙ 18 ∙ 14 = 6 ∙∗∙ 7 to make it correct?
5.
How many possible routes are there to go from A to B in the direction indicated by the arrows?
6.
Martha multiplied two 2-digit numbers correctly on a piece of paper. Then she scribbled out three digits as shown.

What is the sum of the three digits she scribbled out?
7.
A large rectangle is made up of nine identical rectangles whose longest sides are 10 cm long. What is the perimeter of the large rectangle?

8.
A hotel on an island in the Caribbean advertises using the slogan "350 days of sun every year!''. According to the advert, what is the smallest number of days Willi Burn has to stay at the hotel in 2018 to be certain of having two consecutive days of sun?
9.
The diagram shows a rectangle of dimensions 7 × 11 containing two circles each touching three of the sides of the rectangle. What is the distance between the centres of the two circles?

10.
Only one of the digits in the year 2018 is a prime number. How many years will pass till the next year when all of the digits in the year number are prime numbers?
11.
Part B: Each correct answer is worth 4 points
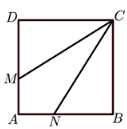
Square ABCD has sides of length 3 cm. The points M and N lie on AD and AB so that CM and 퐴퐴CN split the square into three pieces of the same area. What is the length of DM?
12.
A rectangle is divided into 40 identical squares. The rectangle contains more than one row of squares. Avacoloured the middle row. What is the largest possible number of squares that remain uncoloured?
13.
A lion is hidden in one of three rooms. A note on the door of room 1 reads "The lion is here". A note on the door of room 2 reads "The lion is not here". A note on the door of room 3 reads "2 + 3 = 2 × 3". Only one of these statements is true. In which room is the lion hidden?
14.
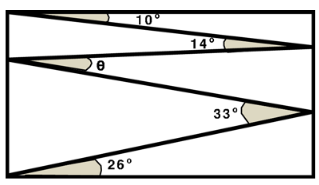
Valeriu draws a zig-zag line inside a rectangle, creating angles of 10°, 14°, 33°, and 26° as shown. What is the size of angle
?
15.
Using only the digits 1, 2, 3, 4, and 5 exactly once, Alice wrote several prime numbers less than 100. She also noticed that there was more than one way to do that, with one prime number being always in the list. What is this number?
16.
The diagram shows a rectangle and a line X parallel to its base. Two points A and B lie on X, as shown (A is outside and B is inside the rectangle). The sum of the areas of the two shaded triangles is 10 cm
2.
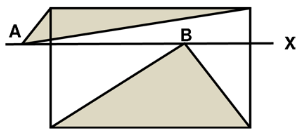
What is the area of the rectangle?
17.
James wrote a different integer from 1 to 9 in each cell of a 3 × 3 table. He calculated the sum of the integers in each of the rows and in each of the columns of the table. Five of his sums are 12, 13, 15, 16 and 17, in some order. What is his sixth sum?

18.
Eleven points are marked from left to right on a straight line. The sum of all the distances between the first point and the other points is 2018. The sum of all the distances between the second point and the other points, including the first one, is 2000. What is the distance between the first and second points?
19.
When Mark begins a journey, his car odometer shows a palindromic number 29792 km. (Palindromic numbers remain the same when written forwards or backwards.) At the end of the journey, 3 hours later, the odometer shows another palindromic number. Mark is a responsible driver, respects the traffic rules and knows that his average speed has not exceeded 100 km/h. What is the maximum average speed that Mark could have recorded?
20.
Yesterday, 17.03.2018, was John's birthday. Now his age is equal to the sum of the digits of the year he was born. How old is John?
21.
Part C: Each correct answer is worth 5 points
There are three candidates for one position as class supervisor and 130 students are voting. Suhaimi has 24votes so far, while Khairul has 29 votes and Akmal has 37 votes. How many more votes does Akmal need in order to receive more votes than any of the two other candidates?
22.
The diagram shows a net of an unfolded rectangular box. What is the volume of the box?

23.
Ria wants to write a number in every cell on the border of a 5 × 6 table. In each cell, the number she will write must be equal to the sum of the two numbers in the cells with which this cell shares an edge. Two of the numbers are given in the diagram. What number will she write in the cell marked by x?

24.
Simon and Ian decide to have a race. Simon runs around the perimeter of the pool shown in the diagram while Ian swims lengths of the pool (50 m each). Simon runs three times faster than Ian swims. Ian swam six lengths of the pool in the same time Simon ran around the pool five times. How wide is the pool?

25.
Azmi, Burhan and Choo went shopping. Burhan spent only 15% of what Choo spent. However, Azmi spent 60% more than Choo. Together they spent $55. How much did Azmi spend?
26.
Freda's flying club designed a flag of a flying dove on a square grid as shown. The area of the dove is 192 cm2. All parts of the perimeter of the dove are either arcs of a circle or straight lines. What are the dimensions of the flag?

27.
Points N, M and L lie on the sides of the equilateral triangle ABC, so that
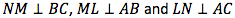
as shown in the diagram
The area of triangle ABC is 36. What is the area of triangle LMN?
28.
The average weight of six members of the women’s track and field competitive team is 60 kg. When twonew athletes, Ann and Sophie, are included in the team the average weight of the group decreases to 58 kg.Ann is 8 kg heavier than Sophie. What is the weight of Ann, in kg?
29.
Write nine different positive integers, one in each circle in the diagram, such that the product of the threenumbers along any line is the same and also the least possible.
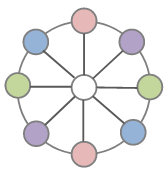
What is the least possible value of the product?
30.
n isosceles triangle ABC, points K and L are located on sides AB and BC respectively so that AK =KA = LB and KB = AC.
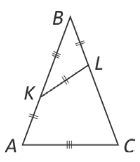
What is the size of angle ABC?