1.
Part A: Each correct answer is worth 3 points
What is the time 17 hours after 17:00?
2.
A group of girls stands in a circle. Xena is the fourth on the left from Yana and the seventh on the right from Yana. How many girls are in the group?
3.
The sum of 2017 nonnegative integers is 2016. What is the product of the numbers?
4.
The diagram shows a stripy isosceles triangle and its height. Each stripe has the same height. What fraction of the area of the triangle is white?

5.
The diagram shows two rectangles whose sides are parallel. What is the difference between the perimeters of the two rectangles?

7.
The sum of three different positive integers is 7. What is the product of these three integers?
8.
The diagram shows four overlapping hearts. The areas of the hearts are 1 cm
2, 4 cm
2, 9 cm
2 and 16 cm
2. What is the grey area?

9.
There are nine houses in a row on Deer Street. At least two people live in every house. There are no two neighbouring houses where more than ten people live altogether. What is the maximum number of people who can live in the nine houses?
10.
Yvonne has 20 dollars. Each of her four sisters has 10 dollars. How many dollars does Yvonne have to give to each of her sisters so that each of the five girls has the same amount of money?
11.
Part B: Each correct answer is worth 4 points 11.Annie the Ant started at the left end of a pole and crawled ଶଷ of its length. Bob the Beetle started at the right end of the same pole and crawled ଷସ of its length. What fraction of the length of the pole are Annie and Bob now apart?

12.
In the diagram, the dashed line and the black path form seven equilateral triangles. The length of the dashed line is 20 cm. What is the length of the black path, in cm?

13.
Four cousins Ema, Iva, Rita and Zina are 3, 8, 12 and 14 years old, although not necessarily in that order. The sum of the ages of Zina and Ema is divisible by 5. The sum of the ages of Zina and Rita is also divisible by 5. How old is Iva?
14.
This year in the Kangaroo Hop exactly 35% of the runners were women and there were 252 more men than women. How many runners were there in total?
15.
Simon wanted to cut a long wooden stick into nine pieces of the same length. He marked the positions of the cuts; however, he did not have the time to cut the stick. Barbara wanted to cut the same stick into only eight pieces of the same length and, without seeing the marks made by Simon, marked the positions where she had to cut. However, she also postponed cutting the stick for later. Meanwhile Carl took the stick and cut it along all marks he saw. How many pieces did Carl obtain?
16.
Two segments, each 1 cm long, are marked on opposite sides of a square of side 8 cm. The ends of the segments are joined as shown in the diagram.
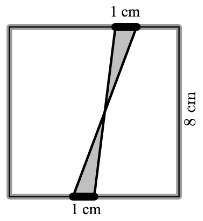
What is the shaded area, in cm
2?
17.
Tycho wants to prepare a schedule for his jogging. He wants to jog exactly twice a week, and on the same days every week. He never wants to jog on two consecutive days. How many such schedules are possible?
18.
If students are late for school, they are punished by detention. First late arrival means 10-minute detention, the second one 20 minutes after school, the third one 30 minutes, the fourth one 40 minutes etc. In winter term, Simon had to spend extra 9 hours and 10 minutes at school. How many times was he late?
19.
In 16 years Dana will be five times older than she was four years ago. In how many years will Dana celebrate her 16th birthday?
20.
Emily wants to write a number into each cell of a 3 × 3 table so that the sums of the numbers in any two cells that share an edge are the same. She has already written two numbers, as shown in the diagram. What is the sum of all the numbers in the table?

21.
Part C: Each correct answer is worth 5 points
The measures of the angles in a triangle, in degrees, are three different integers. What is the minimum possible sum of its smallest and largest angles?
22.
Buses leave the airport every 3 minutes to drive to the city centre. A car leaves the airport at the same time as one bus and drives to the city centre by the same route. It takes each bus 60 minutes and the car 35 minutes to drive from the airport to the city centre. How many buses does the car pass on its way to the centre, excluding the bus with which it left?
23.
Olesia's tablecloth has a regular pattern, as shown in the diagram. What percentage of the tablecloth is black?

24.
The product of three consecutive numbers is 23∙33∙7∙13. What is the sum of these three numbers?
25.
A sequence of digits is obtained in the following way: The first two digits are 2 and 3 and each digit afterwards is the units’ digit of the product of the two preceding digits in the sequence. The first several digits in the sequence are 2, 3, 6, 8, 8, ..... What is the 2017th digit in the sequence?
26.
Mike had 125 small cubes. He glued some of them together to form a big cube with nine tunnels leading through the whole cube as shown in the diagram. How many of the small cubes did he not use?

27.
How many natural numbers N have the property that among the numbers 1, 2, ...., N exactly 30% are divisible by 3?
28.
Two runners are practicing on a 720-metre circular track. They run in opposite directions, each at a constant speed. The first runner needs four minutes to complete the full loop and the second runner needs five minutes. How many metres does the second runner travel between two consecutive meetings of the two runners?
29.
Sarah wrote a natural number in each of the five boxes in the bottom row of the diagram. Then she wrote in each of the other boxes the sum of the two numbers in the boxes immediately underneath. What is the maximum number of odd numbers that could appear in the completed diagram?

30.
The diagram shows a parallelogram ABCD with area S. The intersection point of the diagonals of the parallelogram is O. The point M is marked on DC. The intersection point of AM and BD is E and the intersection point of AC and BM is F. The sum of the areas of the triangles AED and BFC is 1/3 S. What is the area of the quadrilateral EOFM, in terms of S?
