1.
Part A: Each correct answer is worth 3 points
How many whole numbers are there between 3.17 and 20.16?
3.
Dalila is blowing out the candles on her birthday cake. On her first attempt, she blows out three quarters of the candles. On her second try she blows out the remaining four candles. How many candles are on Dalila’s birthday cake?
4.
What is the sum of the two angles marked by 1 and 2?

5.
Jenny had to add 26 to a certain number. Instead she subtracted 26 and obtained –14. What number should she have obtained?
7.
The product of 2016 positive integers is 3. Which of the following is their sum?
8.
Two pieces of rope have length 1 m and 2 m. Alex cuts the pieces into several parts. All the parts have equal length. Which of the following could not be the total number of parts he obtains?
9.
After a party, Jane washed half of the glasses, Alex washed half of the rest and then Sasha washed half of the remaining glasses. There were only three glasses left for David to wash. Half of the guests used one glass each and the other half of the guests used two glasses each. How many people were there at the party?
10.
The diagram shows four identical rectangles placed inside a square.
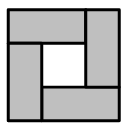
The perimeter of each rectangle is 16 cm. What is the perimeter of the large square?
11.
Part B: Each correct answer is worth 4 points
Four towns P, Q, R and S are connected by roads, as shown. A race must use each road exactly once. The race starts at S and finishes at Q. How many possible routes are there for the race?
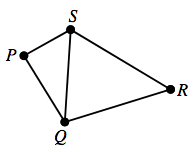
12.
Each letter in the word BENJAMIN represents one of the digits 1, 2, 3, 4, 5, 6 or 7. Different letters represent different digits. The number BENJAMIN is odd and divisible by 3. Which digit corresponds to the letter N?
13.
The sum of five different positive integers is 17. How many different values can their product take?
14.
Ivor writes down the results of the quarter-finals, the semi-finals and the final of a direct-elimination tournament. The results are (not necessarily in this order): Bart beat Antony; Carl beat Damien; Glen beat Henry; Glen beat Carl; Carl beat Bart; Ed beat Fred; and Glen beat Ed. Who played in the final?
15.
Tonight I am meeting five of my friends: Andrew; Boris; Chris; Dan; and Eugene. Andrew has already met one of them, Boris – two of them, Chris – three of them, and Dan – four of them. How many of them has Eugene already met?
16.
Tim, Tom and Jim are triplets (three brothers born on the same day). Their twin brothers John and James are 3 years younger. Which of the following numbers could be the sum of the ages of the five brothers? (All ages are rounded to a whole year).
17.
Inside a square of area 36, there are shaded regions as shown. The total shaded area is 27. What is the value of p + q + r + s?

18.
Two kangaroos Jum and Per start to jump at the same time, from the same point, in the same direction. They make one jump per second. Each of Jum’s jumps is 6 m long. Per’s first jump is 1 m long, the second is 2 m long, the third is 3 m long, and so on. After how many jumps will Per catch Jum?
19.
In my school, 60% of the teachers get to school by bike, which is 45 teachers. Only 12% of the teachers use their cars to get to school. How many teachers use their cars to get to school?
20.
There are 20 students in a class. They sit in pairs so that exactly one third of the boys sit with a girl, and exactly one half of the girls sit with a boy. How many boys are there in the class?
21.
Part C: Each correct answer is worth 5 points
Twelve girls met in a café. On average, they ate 1.5 cup-cakes. None of them ate more than two cup-cakes and two of them had only mineral water. None of the cup-cakes were shared by the girls. How many girls ate two cup-cakes?
22.
Theo’s watch is 10 minutes slow, but he believes that it is 5 minutes fast. Leo’s watch is 5 minutes fast, but he believes that it is 10 minutes slow. Looking at his watch, Theo believes it is now 12:00. What time does Leo think it is now?
24.
Three equilateral triangles are cut from a larger equilateral triangle of perimeter 60 cm. The perimeter of the resulting shape F is 40 cm. What is the sum of the perimeters of the triangles that are cut out?

25.
Several distinct positive integers are written on a blackboard. The product of the smallest two of them is 16. The product of the largest two is 225. What is the sum of all the integers?
26.
A 3 cm wide rectangular strip of paper is dark grey on one side and white on the other. Maria folds the strip, as shown. The dark grey shaded trapezoids are identical.
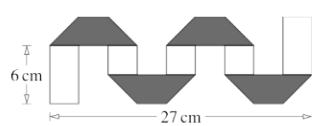
What is the length of the original strip?
27.
Mr. Cook bought a big box of his favourite Halloween candies to hand out to trick-or -treaters. However, he ate half of all the candies himself before the first child came and took her share. He ate half of what was left before the second child came, and half of what was left again before the third child came and took all of the remaining candies. If it is known that each child received the same number of candies, which of the following statements is certainly true about how many candies Mr. Cook originally bought?
28.
The diagram shows an equilateral triangle divided into five regions by lines parallel to one edge. All the regions have the same height. What percentage of the triangle is shaded?

29.
The cube below is divided into 64 small cubes. Exactly one of the cubes is grey, as shown.
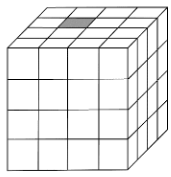
On the first day, the grey cube changes all its neighbouring cubes to grey (two cubes are neighbours if they have a common face). On the second day, all the grey cubes do the same thing. How many grey cubes are there at the end of the second day?
30.
Katie writes 14 different positive integers, one on each of the 14 cubes in the pyramid. The sum of the nine integers written on the bottom cubes is equal to 50. The integer written on each other cube is equal to the sum of the integers written on the four cubes underneath it. What is the greatest possible integer that can be written on the top cube?
