2.
Which of the following numbers is closest to 2.015 × 510.2?
3.
The net of a cube with numbered faces is shown in the diagram.Sasha correctly adds the numbers on opposite faces of this cube.What three totals does Sasha get?

4.
A journey from Košice to Poprad through Prešov lasts 2 hours and 10 minutes. The part of the journey from Košice to Prešov lasts 35 minutes. How long does the part of the journey from Prešov to Poprad last?
5.
A triangle has sides of lengths 6, 10 and 11. An equilateral triangle has the same perimeter.What is the side length of the equilateral triangle?
6.
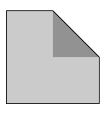
One corner of a square is folded to its centre to form an irregular pentagon. The areas of the pentagon and of the square are consecutive integers. What is the area of the square?
7.
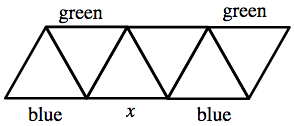
The diagram indicates the colours of some unit segments of a pattern. Luis wants to colour each remaining unit segment in the pattern either red or blue or green. Each triangle must have one side of every colour. What colour can he use for the segment marked x?
8.
A soccer club owns five identical mowers. It takes 10 hours to mow the grass of the soccer field using two of the mowers. How long does it take to mow the grass of the same field using all five mowers?
9.
How much faster does the second hand of a circular clock make one complete rotation compared to the hour hand of the same clock?

10.
A cyclist rides at 5 m per second. The wheels of his bicycle have a circumference of 125 cm.How many complete turns does each wheel make in 5 seconds?
11.
Part B: Each correct answer is worth 4 points
In a class, no two boys were born on the same day of the week and no two girls were born in the same month. Were a new boy or a new girl to join this class, one of these two conditions would no longer be true. How many children are there in the class?
12.
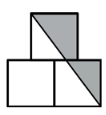
In the figure, each square has sides of length 1. What is the area of the shaded region?
13.
Every asterisk in the equation 2∗0∗1∗5∗2∗0∗1∗5∗2∗0∗1∗5 =0 is to be replaced with either + or − so that the equation is correct. What is the smallest number of asterisks that must be replaced with +?
14.
A bush has 10 branches. Each branch has either 5 leaves only, or 2 leaves and 1 flower.Which of the following could be the total number of leaves the bush has?

15.
Rachel added the lengths of three sides of a rectangle and got 44cm. Heather added the lengths of three sides of the same rectangle and got 40cm. What is the perimeter of the rectangle?
16.
A bowl contains only 3 red marbles and 3 blue marbles. All of them are identical in size and shape. Ann and Bill play the following game: First, Ann takes one marble out of the bowl, with her eyes closed. Then, Bill takes one marble out of the remaining ones in the bowl, with his eyes closed. Ann wins the game if the two marbles are of different colours, and Bill wins the game if the two marbles are of the same colour. In how many different ways can Bill win the game?
17.
The mean score of the students who took a mathematics test was 6. Exactly 60% of the students passed the test. The mean score of the students who passed the test was 8. What was the mean score of the students who failed the test?
18.
Ria wants to write a number in each of the seven bounded regions in the diagram. Two regions are neighbours if they share part of their boundary. The number in each region is to be the sum of the numbers in all its neighbours. Ria has already written in two of the numbers, as shown.
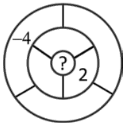
What number must she write in the central region?
19.
n the triangle ABC of area 120 cm2, the ratio between the lenght of one side and the corresponding height is 3:5. What is this height, in cm?
20.
Albert and Ben each have several marbles. If Albert gives 6 of his marbles to Ben, they will have the same number of marbles. If Albert gives a half of his marbles to Ben, then Ben will have 8 marbles more than Albert will have. How many marbles in total do the boys have?
21.
Part C: Each correct answer is worth 5 points
A square with area 30 cm2 is divided in two by a diagonal and then into triangles, as shown.The areas of some of these triangles are given in the figure.
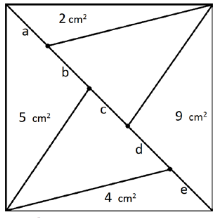
Which part of the diagonal is the longest?
22.
In a group of kangaroos, the two lightest kangaroos weigh 25% of the total weight of the group.The three heaviest kangaroos weigh 60% of the total weight. How many kangaroos are there in the group?
23.
In the trapezoid PQRS, the sides PQ and SR are parallel. Angle RSP is 120° and RS =SP = 1/3 PQ. What is the size of the angle PQR?
24.
In the trapezoid ABCD, the points M and N are the midpoints of the sides BC and CD, respectively.
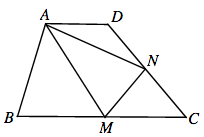
The area of ABCD is 32cm
2 and the length of AD is 1/3 of the length of BC. What is the area of the triangle AMN, in cm
2?
25.
Three cats, Tom, Bob and Rob, kept a record on the number of mice each of them caught for three consecutive days. Each day, Tom caught twice as many mice as in the previous day; Bob caught two more mice than in the previous day, while Rob caught the same number of mice each day. In the end, it appeared that each cat caught the same number of mice in total. At least how many mice did Tom, Rob and Bob catch together in the first day?
26.
Consider a rectangle whose side lengths are prime numbers and the perimeter equals 100. How many different values can the area of such rectangle take?
27.
Five points lie on a line. Alex finds the distances between every possible pair of points. He obtains, in increasing order, 2, 5, 6, 8, 9, k, 15, 17, 20 and 22. What is the value of k?
28.
Five positive integers (not necessarily all different) were written on five cards. Peter calculated the sum of the numbers on every pair of cards. He obtained only three different totals, 57, 70, and 83. What is the largest of the five integers on the cards?
29.
In my phone book, the telephone number of my friend Ekin has six digits, but it must be a seven-digit number as are all phone numbers in his area. I have no idea what digit I forgot to write down, or its position in the number. How many numbers do I have to dial to be certain that I will call Ekin’s number? (Note that in Ekin’s area phone numbers may start with any digit, including 0).
30.
Mary divides 2015 correctly by 1, 2, 3, and so on, up to and including 1000. She writes down the remainder for each division. How many of these remainders are greater than 600?