1.
There are two clocks in Cathy's room. One of t hem is 25 minutes behind. Now it is showing 7: 40. The second clock is 15 minutes ahead. What is the second clock showing now ?
3.
Father hangs the laundary outside on a clothesline. He wants to use as few pegs as possible. For three towels he needs four pegs, as shown. How many pegs does he need for eleven towels?

4.
A math class lasts 45 minutes. Peter can solve any problem from the textbook in exactly 6 minutes.However, he needs one minute rest after solving each problem.How many problems can Peter solve completely during one math class?
5.
Fifteen children are playing hide and seek. One of them is the "seeker". After a while seven children were still hiding. How many children have already been found?
6.
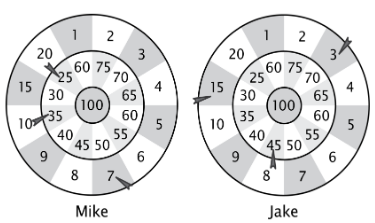
Mike and Jake were playing darts. Each one threw three darts (see the picture). Who won, and by how many points did he win?
7.
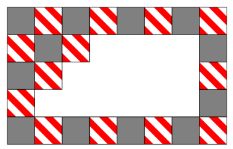
A regular rectangular pattern on a wall was created with two kinds of tiles: grey and striped. Some tiles have fallen off the wall (see the picture). How many grey tiles have fallen off?
8.
The year 2012 is a leap year, that means there are 29 days in February. On the 15th of March 2012, the ducklings of my grandfather are 20 days old. When did they hatch from their eggs?
9.
Part B: Each correct answer is worth 4 points
You have L - shaped tiles, each consisting of four squares as shown:
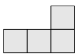
.
How many of the following shapes can you make by glueing together two of the given tiles?
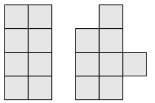
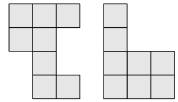
10.
Once Little Piggy planted 8 acorns. In a few years, oak trees grew from all acorns except two of them. All oak trees except two of them had their acorns. Acorns from all profilic trees except one, are very tasty. How many oaks with tasty acorns are there?
11.
In a sudoku the numbers 1, 2, 3, 4 can occur only once in each column and once in each row. In the mathematical sudoku on the picture, Patrick first writes in the results of the calculations. Then he completes the sudoku. Which number will Patrick put in the grey cell?

12.
Grandmother made 20 gingerbread biscuits for her grandchildren. She decorated them with raisins and nuts. First she decorated 15 biscuits with raisins and then 15 biscuits with nuts. At least how many biscuits were decorated both with raisins and nuts?
13.
Among Nikolay's classmates there are twice as many girls as there are boys. Which of the following numbers may be equal to the number of all children in this class?
14.
In the animal's school, three kittens, four ducklings, two goslings and several lambs are taking lessons. The teacher owl found out that all of her pupils have 44 legs altogether. How many lambs are among them?
15.
In one kangaroo family, there is a custom to name their babies by names, which consist of two letters of the word KANGAROO: the first letter is a consonant, the second letter is a vowel. How many different baby names can be composed?
16.
At a Christmas party, there was exactly one candlestick on each of the 15 tables. There were six five-branched candlesticks, and the rest were three-branched ones. How many candles had to be bought for all the candle sticks?
17.
Part C: Each correct answer is worth 5 points
The figure consists of an equilateral triangle, a square and a regular pentagon. It is built by sticks of equal length. At most many such figures can be built wit h a box of 2012 sticks of equal length ?
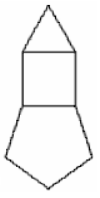
18.
Gregor forms two numbers with the digits 1, 2, 3, 4, 5 and 6. Both numbers have three digits, and each digit is used only once. Gregor adds these two numbers. What is the greatest sum Gregor can obtain ?
19.
Laura, Iggy, Val and Kate want to be in one photo together. Kate and Laura are best friends and they want to stand next to each other. Iggy wants to stand next to Laura because h e likes her. In how many possible ways can they arrange for the photo?
20.
A grasshopper wants to climb a staircase with many steps. She can make only two kinds of jumps: three steps up , or four steps down. Beginning at th e ground level, at least how many jumps will she have to make in order to take a rest on the 22
th step?
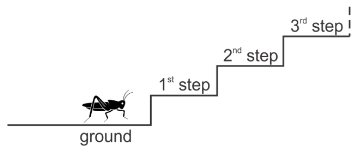
21.
Frank made a domino snake of seven tile s. He put the tiles next to each other so that the sides with the same number of dots touch ed . Originally the snake had 33 dots on its back. However, Frank's brother George took away two tiles from the snake (see the picture).
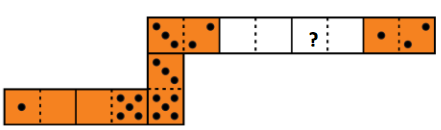
How many dots were in the place with the question mark?
23.
A rectangular paper sheet measures 192 × 84 mm. You cut the sheet along just one straight line to get two parts, one of which is a square. Then you do the same with the non - square part o f the sheet, and so on. What is the length of the side of the smallest square you can get with this procedure?
24.
In a soccer game the winner gains three points, while the loser gains zero points. If the game i s a draw, then the two teams gain one point each. A team has played 38 games and gain ed 80 points. Find the greatest possible number of games that the team lost.